題目

題目大意

有一顆樹，節點樹為 N，每個節點上都會有一個數字，保證節點的數字和為 N。每次可以對把任意節點上的數字移動 1 點到 children 和 parent，問最少移動幾次可以使每個節點上的數字都恰好為 1。

想法

觀察一下應該不是什麼 DP 題，蠻直覺的遞迴解。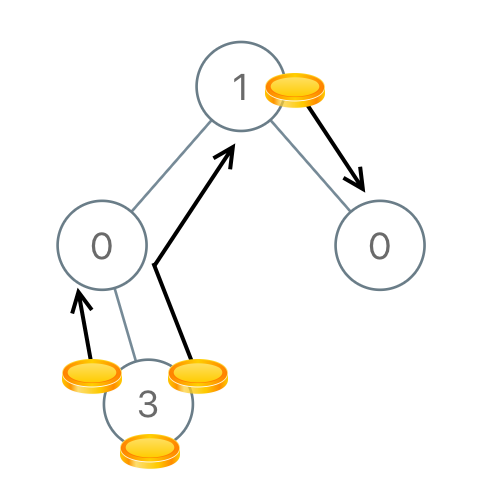

以這張圖來說的話，3 明顯多了 2，可以先考慮移動兩次到他的 parent，接著他的 parent 會多 1，所以還要移動一個到 parent，右邊的子樹計算後總共少了 1，我們只要能移動 1 到右子樹就好。
但這樣的想法寫成 code 應該會有人卡在「遞迴回傳的是這個節點代表的子樹多了/少了多少數字」不知道如何計算答案，基本上多傳一個紀錄答案的變數的 reference 就可以解決了，也可以開個 class 裡的變數直接當全域用。

Code(C++)

int dfs(TreeNode* root, int& cnt) {
    if (!root) return 0;
    int L = dfs(root->left, cnt), R = dfs(root->right, cnt);
    cnt += abs(L) + abs(R);
    return root->val + L + R - 1;
}
int distributeCoins(TreeNode* root) {
    int ans = 0;
    dfs(root, ans);
    return ans;
}

心得

好像 tree 的一般遞迴題普遍都被放在 medium，明天試試看 pick one 到 hard 為止好了，不然有點水我良心不安。